“Circle theorems” is a hard-tier topic that many IGCSE math students find challenging. If you are looking to achieve a grade 8-9 for the exam, then being able to handle the Circle Theorem confidently is useful. I am writing this blog post to share where many students go wrong and some important strategies you should follow to solve circle theorem questions easily.

Know your circles!

You may be able to label various parts of circles through visual inspection, but you must be able to distinctly describe each of these components.

Take a few minutes and write down simple definitions for the following circle components.

• Diameter
• Radius
• Circumference
• Arc
• Sector
• Segment
• Tangent
• Chord
• Cyclic Quadrilateral

Now check if your definitions for the above help you distinguish the following accurately:

Example – #1

Can you identify which of the following lines (AB, GH, MN) is/are the diameter/s of the circle? Make sure you go by your definition of the diameter.

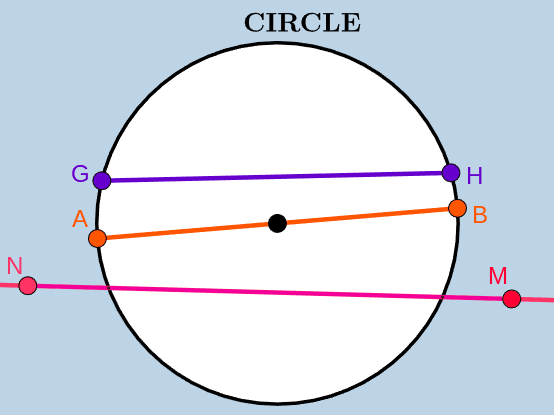
If your definition for diameter was something like “Line across the circle”, “The diameter is half the radius.”, or “line joining two points on the circle”, is not accurate and would not help you distinguish the diameter (i.e AB) in the above diagram.

Example – #2

Next, can you justify with your definitions of “sector” and “segment” which of the following can be classified as a sector?

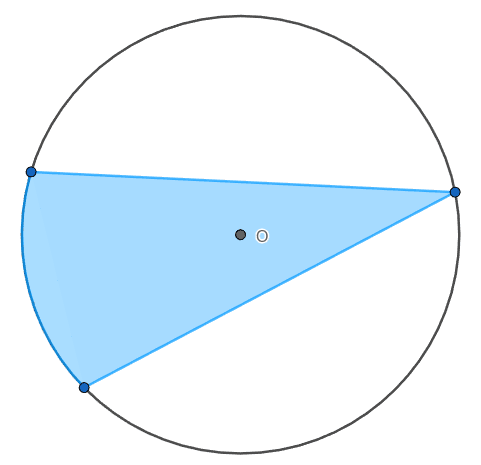
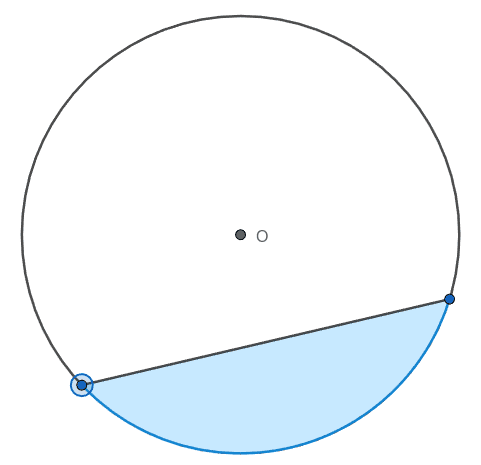
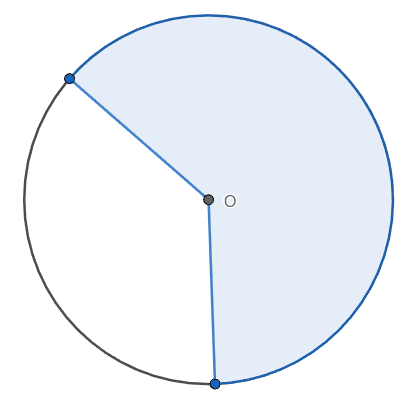
If your understanding of the sector was mostly visual, meaning that you identify sectors as parts of circles, slices of circles, then perhaps you would potentially consider the shaded region of Figure A to be a sector.

Without a precise definition of a sector, it can be difficult to explain the difference between a segment (Figure B) and a sector (Figure C) without resorting to visual examples.

Example – #3

As the third example, I’ve picked one of the most commonly confused elements in circle theorems – cyclic quadrilaterals. Over and over again, examiner reports indicate how students lose marks because they either haven’t identified or misidentified a cyclic quadrilateral.

Could you identify which of the following can be identified as a cyclic quadrilateral?

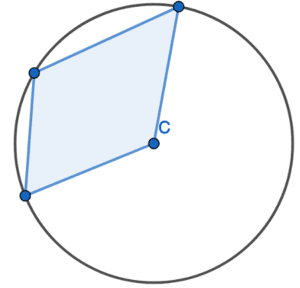
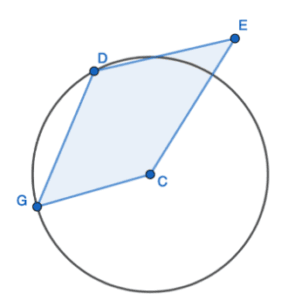
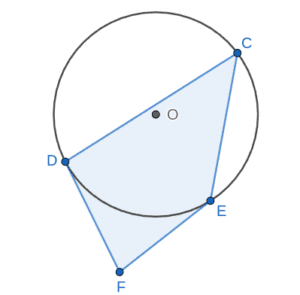
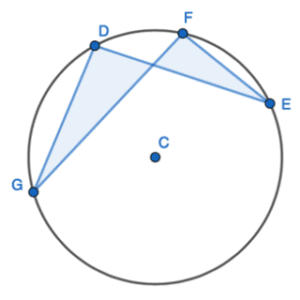
Did you find the cyclic quadrilateral? If you did, then it’s high time you brushed up on the definition of a cyclic quadrilateral because none of the figures above illustrate cyclic quadrilaterals!

I hope the 3 examples above are sufficient to prove my point on the importance of definitions of elements and components of a circle. Below are precise definitions for the circle components:

• Diameter – a straight line that passes through the center of the circle and has its endpoints on the circumference.
• Radius – Distance from the center to the circumference of the circle.
• Circumference – The outer edge of the circle.
• Arc – Part of the circumference of a circle.
• Chord – a straight line that has its endpoints on the circumference.
• Sector – a region of a circle enclosed by two radii and the arc between them.
• Segment – a region of a circle enclosed by a chord and an arc.
• Tangent –
• Cyclic Quadrilateral – 4-sided polygon inside a circle with all 4 vertices on the circumference of the circle.

Understanding not memorizing theorems

You may have all the circle theorems word for word, but as long as you don’t have a deeper understanding of the theorems then you won’t be able to apply the theorems successfully in questions. I’ve picked 5 circle theorems that have the most misconceptions.

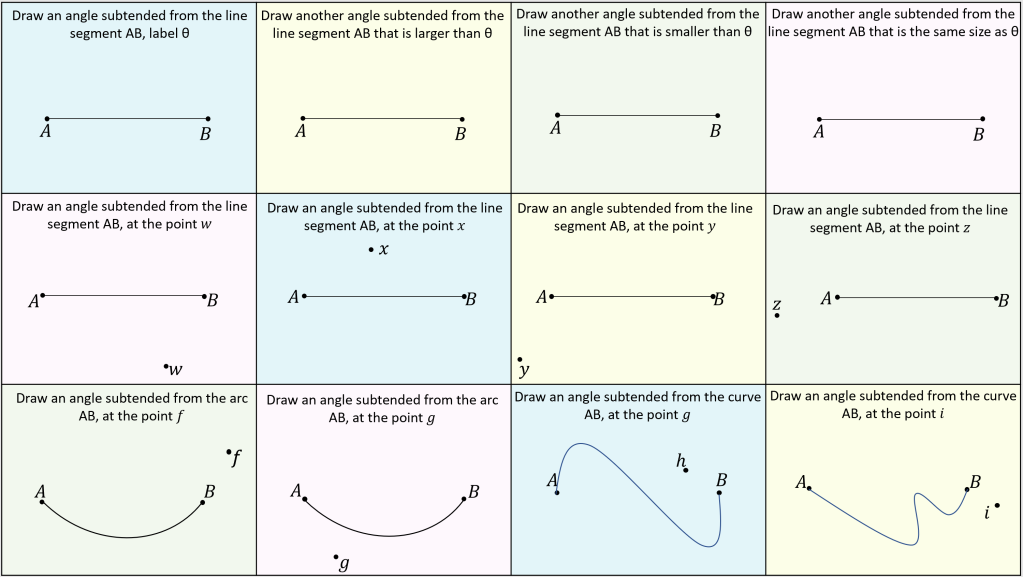
#1 – Angles subtended at the center and circumference

This is a classic theorem that many students use without really understanding it. Especially the term subtended. No one knows what it means but they disregard it as a filler word and go about solving questions until they stumble upon a challenging problem.

I would highly recommend doing this activity on paper to get a deep understanding of what it is to subtend an angle at a point.

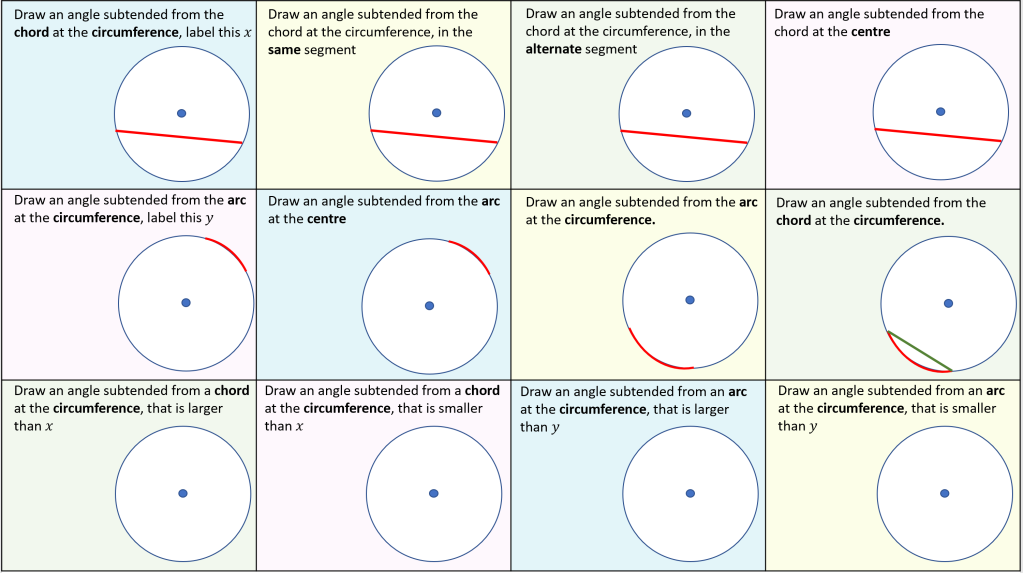
#2 – Angles in the same segment

This is the theorem that most math courses start circle theorems with.

Students often memorize this theorem by recognizing patterns, such as the M or W shape. However, this approach is problematic for several reasons:

1. It can lead to missed applications of the theorem when the M or W pattern isn’t present, meaning the theorem may still apply in different orientations.
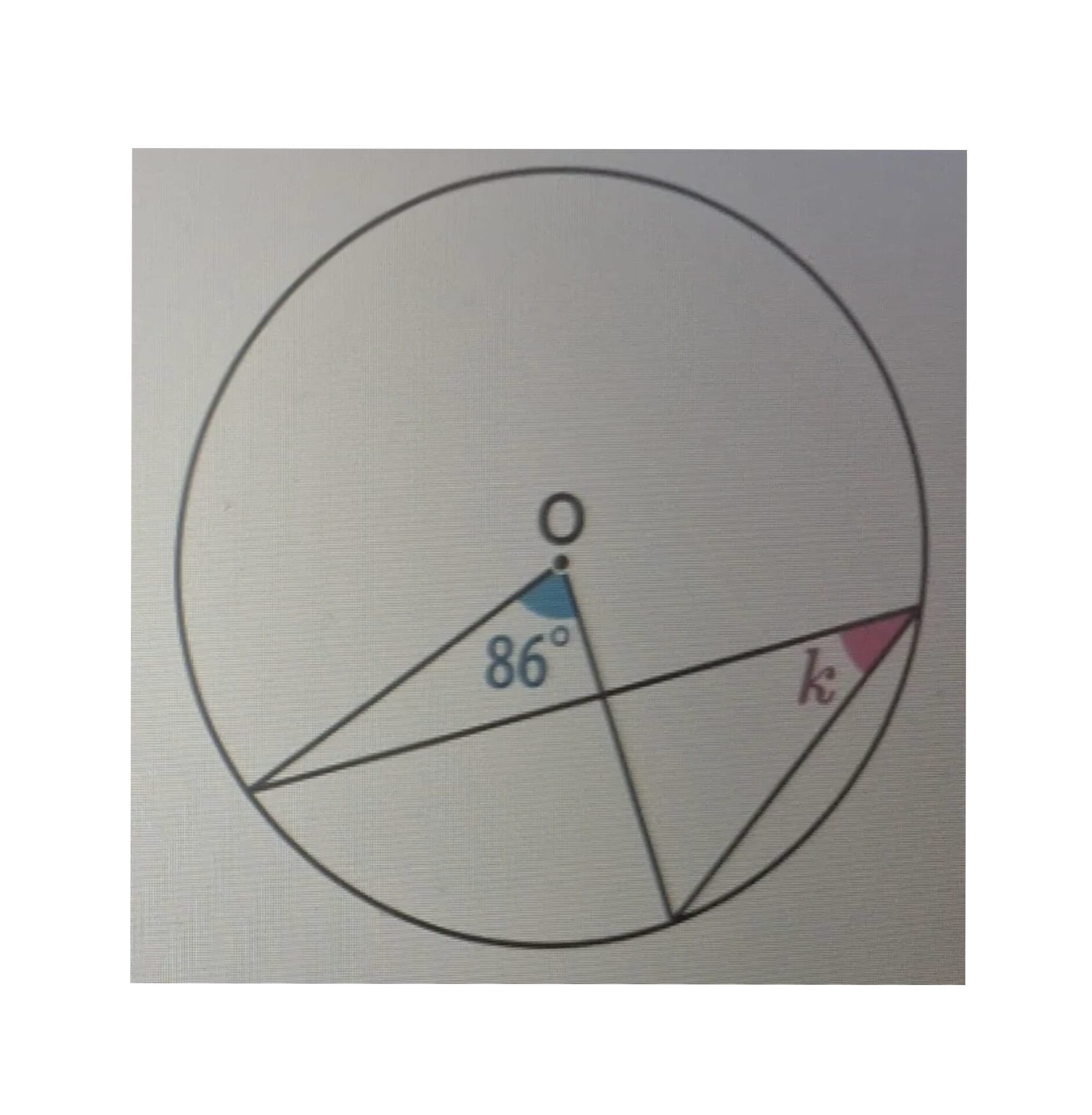
2. It can cause students to mistakenly assume the theorem applies just because they see the M or W pattern, even when it doesn’t. For example, in the question below, the M pattern may lead students to falsely believe that the angle k is 86 degrees.
   
3. It can lead to forgetting the correct terminology. Relying on pattern recognition rather than understanding the actual definitions can hurt your ability to explain your reasoning, which can cost marks in exams.

I get students to engage with the following simulation to build more intuition around the theorem. Try it yourself, and note how the chord CD splits the circle into 2 segments (the blue segment and the red segment). If you interact with the simulation you should clearly understand that the same segment theorem is saying that the angles within a particular segment are always identical.

#3 – The alternate segment theorem

One of the most notorious circle theorems among them all. Unless you understand the theorem well, you will find it extremely difficult to identify and execute the theorem accurately.

Interact with the simulation below to understand exactly how the alternate segment theorem works, and why it is called the “alternate” segment theorem!

Actively look for geometric features

Once you are comfortable with the theorems, it’s time to strategize solving circle theorem problems. As with many geometric problems, I encourage students to actively look for important features such as tangents, diameters, cyclic quadrilaterals, centers, etc.

Identifying these features allows you to narrow down which set of theorems could potentially be helpful. For example, if you notice a chord, and an angle subtended at the center or at the circumference, then you can look for angles in the same segment or the theorem that relates the angle at the center and the angle subtended at the circumference.

Don’t make assumptions on features

In geometry problems, it is very tempting to assume features. Of course, the people setting the exams know this and hence will set up the diagrams to lure you into making such assumptions.

Some of the classic assumptions are of right angles, symmetry, equal lengths, and center of circles.

The only workaround is to force yourself to avoid unfounded assumptions. If you have an inclination regarding a certain property/feature then look for evidence. Evidence may be in the statements of the question, or perhaps other geometry principles may help you prove or disprove your assumption.

Don’t get me wrong, it’s not a bad thing to make guesses based on visual estimation, but once you have a hunch about a certain property make sure to find evidence to back it up.

Hustle the puzzle!

Circle theorem problems are like puzzles—there’s no one-size-fits-all method to solve them. When asked to find a specific angle, don’t expect a single theorem to instantly give you the answer.

Many students get frustrated when they can’t directly find the angle right away, but that’s where perseverance comes in! Instead of giving up, focus on finding other missing angles along the way that will bring you closer to the solution.

Think of geometric problems as puzzles to be solved. Once you adopt this mindset and apply the strategies above, the journey becomes just as rewarding as the answer itself!”