Introduction

You’re likely aware that the math section of the English TOLC-E exam can be quite challenging. To nail a good score in the math section, you need to be effective at time management, and handling difficult math questions.

In this blog post, we’ll cut to the chase. I’ll share practical, no-nonsense strategies that can help you boost your score in the math section.

Please note that these strategies are not gimmicks or tricks, rather they are smart approaches to handling MCQ questions, thus you will be required to apply math principles. Let’s dive right in.

Trial and Error

The trial and error strategy is widely used in MCQ tests. It can be very effective in the TOLC-E exam when used in appropriate questions. Some of the question types this method works best include:

• Solutions to algebraic equations
• Determining the domain of functions
• Numbers and reasoning

With trial and error, you test each solution to validate the result. Below is an example of applying trial and error.

Example of Using Trial and Error

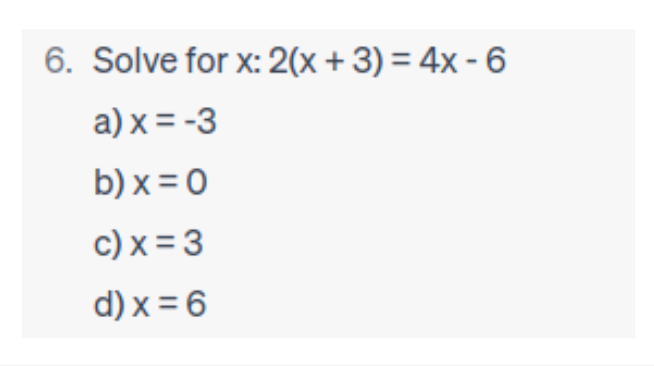
When trying option a) x = -3, we can substitute it in the equation as follows:
$4(-2-2) = (8\times{-2}) + 4 $
Simplifying the left-hand side and right-hand side we get:
$$\displaylines{
4\times{-4} = -16 + 4\\-16 = -16 + 4\\ -16 = -12}
$$
Since we got a false statement, we can verify through trial and error that a is incorrect. Similarly, you’d have to test the other answer options until you get a true statement.

In this question, you will see that the last option d works for the equation.
$$
\displaylines{
2\times(6+3) = (4\times{6}) – 6\\
2\times{9} = 24 – 6\\
18 = 18
}
$$

In the worst-case scenario, you may have to test all answer options to obtain the correct option. So I recommend that you use trial and error as a last resort only when you have no idea how to solve the problem.

Elimination I

Elimination is a very powerful strategy with MCQ-style questions. Elimination is a time-saving strategy, but it requires solid reasoning skills to successfully eliminate incorrect choices.

It is quite common to use trial and error and elimination in combination. The following example shows how this strategy is applied.

Example of Using Elimination

Here, we can start with trial and error. There are several options we can choose as a trial. I will go with x = 0, and check whether it is a solution to the equation.
$$\displaylines{
\frac{(x^2 + 2x + 1)(x – 1)}{x + 1} = 0\\
\frac{(0^2 + (2\times{0}) + 1)(0 – 1)}{0 + 1} = 0\\
\frac{1\times{-1}}{1} = 0\\
-1 = 0
}
$$
Since we got a false statement after simplification, this means that 0 cannot be a solution to the equation, thus we can eliminate options A and E.
Next, I am going to test x = -1.

$$\displaylines{
\frac{(x^2 + 2x + 1)(x – 1)}{x + 1} = 0\\
\frac{[(-1)^2 + (2\times{-1}) + 1](-1 – 1)}{-1 + 1} = 0\\
\frac{(1 + -2 + 1)\times{-2}}{0} = 0\\
\frac{0}{0} = 0
}
$$
This is a classic example where you need to have an idea of mathematical principles. Some students have the misconception that $\frac{0}{0}$ is equivalent to 0, but this is not the case. Division by 0 is undefined, hence $\frac{0}{0} \neq 0$.

So, we now know that x = -1 is not a valid option, thus we can eliminate options B and C. Although the elimination of option B is straightforward, it requires good reasoning to understand that option C ($x \neq 0$) includes -1, thereby making it incorrect.
We successfully used elimination to isolate one option, D, which is the correct answer.

Elimination II (with samples)

Another form of elimination is incorporating the use of samples. The method involves the use of actual numbers (samples) to replace unknown quantities/variables. This strategy is especially useful when dealing with questions involving inequalities or number properties.

Example of Using Elimination (with Samples)

Consider the question given below:

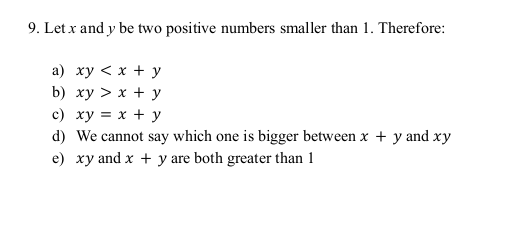
Here, we have two unknowns x and y. But we are given that they are two positive numbers smaller than 1. So, we can use decimal numbers/fractions between 0 and 1. When choosing decimals it’s always best to use decimals that are easy to perform calculations with. I will choose 0.1 and 0.5 for x and y respectively.

If we observe the answer options, it is a comparison of $xy$ and $x + y$. Now, let’s evaluate these expressions using sample values for x and y.
$$\displaylines{
xy = 0.1 \times 0.5\\
xy = 0.05\\
x + y = 0.1 + 0.5\\
x + y = 0.6
}
$$
Now, we can clearly eliminate options b, c, and e.

Option d is a bit tricky, and it requires you to prove your results were not just a coincidence. For this, you have to choose extreme samples and repeat the process. For example, check for x = 1 and y = 1, or x = 0.1 and y = 0.1, etc.. But you should see that the $xy < x + y$ holds true, therefore option a is correct.

Reverse verification

Reverse verification is another effective method of solving questions in the TOLC-E math section. You can use this strategy with questions that require the identification of equivalent expressions.

The procedure is to start with the expressions in the answer options and try to manipulate or simplify the expressions, and see if we can match it with the expression in the question.

Example of Using Reverse Verification

Students find the following sample question challenging because there are multiple routes of simplification if you start with the expression in the question.

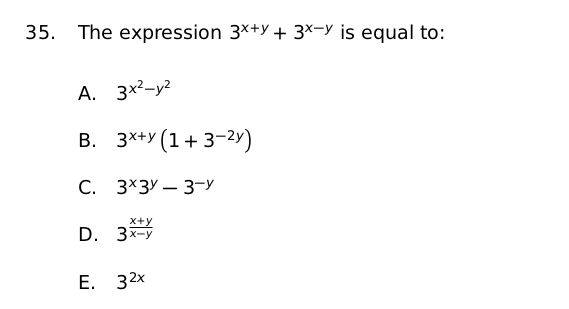
Let’s start with option A:
$$\displaylines{
3^{x^2 – y^2}\\
\text{There are several simplifications that can be done here:}\\
3^{x^2 – y^2} = \frac{3^{x^2}}{3^{y^2}}\\
\text{But, you should realize it is impossible to match with the original expression}\\
}
$$

Now let’s try option B:
$$\displaylines{
3^{x + y}(1 + 3^{-2y})\\
\text{We can expand this by applying the laws of exponents}\\
3^{x + y}(1 + 3^{-2y}) = 3^{x + y} + (3^{x + y}\times 3^{-2y})\\
= 3^{x + y} + 3^{x + y -2y}\\
= 3^{x + y} + 3^{x – y}\\
\text{There’s a match! Therefore, option B is the correct answer.}\\
}
$$

Conclusion

In closing, we’ve explored effective strategies for conquering the math section of the TOLC-E exam. These tools—Trial and Error, Elimination, and Reverse Verification—are valuable assets in your test-taking toolkit. However, remember that they’re not meant to replace a strong foundation in math concepts but to complement it.

As you prepare for the TOLC-E, it’s essential to prioritize building a solid understanding of mathematical principles. To further bolster your readiness, consider enrolling in our TOLC-E preparation sessions. Here, you’ll be able to get personalized math sessions to boost your math score and increase your chances of being accepted for your desired degree course.